子供が持ち帰った小学5年生の算数の問題が結構難しかった
小学5年生の子供が持ち帰った「数字を記号であらわした」算数の問題がなかなか難しいと話題になっています。
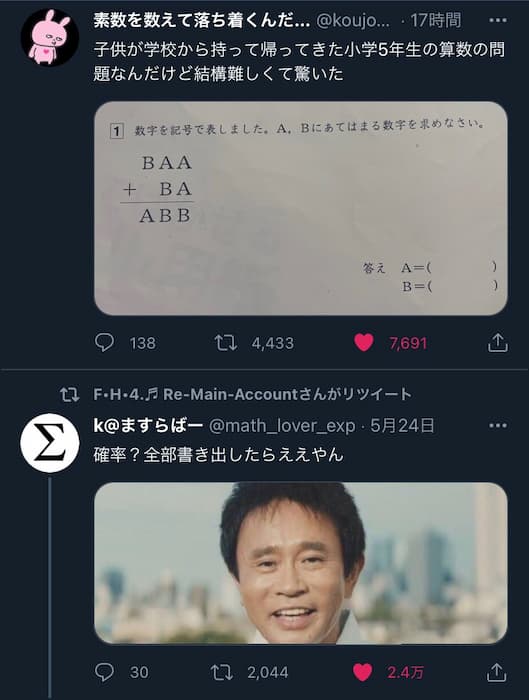
子供が学校から持って帰ってきた小学5年生の算数の問題なんだけど結構難しくて驚いた pic.twitter.com/UMFJ5uhRN7
— 素数を数えて落ち着くんだ… (@koujounodenki) May 25, 2021

ネットの反応
アホやからわからんけど
211
+ 21
122
A=1
B=2— 葵 蒼狐「あおこん」 (@aokon_n1018) May 26, 2021
〈解法その1〉・・・ 愚直に解く
(100B+10A+A)+(10B+A) = 100A+10B+B
整理すると、8A=9B ・・・①
ここで百の位に注目すると、A+1=B ・・・②
①・②より、A=9、B=8 ・・・(答え)— Tatsu 1126 (@Tatsu_pastime) May 26, 2021
小学生ならこんな感じでしょうか。 pic.twitter.com/MtRdrt1Jdx
— @next→電験一種('21) (@godash_sp) May 25, 2021

・100の位をみると下から繰り上がってるから B+1=A
・1の位をBの式にすると B+1+B+1= ?B、増えてるのに一致するには繰り上がるしかないのでB*2+2=10+B, B+2=10だからB=8, A=B+1=9
小学生の知識かどうかはわからない…— KOIZUKA, Akihiko (@koizuka) May 26, 2021
Bは偶数、AはBより1大きい数字、よって奇数
(足し算では1以上の数字は繰り上がらない)AとBを足すと繰り上がってるから10を超える。つまりBは6以上。あとはAの2倍の一桁部分がBになるものを探すだけ、Bの候補は6と8のみ、
と考えていけば、方程式はいらないです。— 山中あきら@おきらく忍伝ハンゾー電子版出てますよ (@chiku012) May 26, 2021
この方法はどうです? pic.twitter.com/AMrLhfXaaj
— yoshi_ozawa (@osk_ni_yoshi) May 26, 2021

3桁目のBがAになっている。足し算でB→Aになるのは繰り上げしか考えられないので
A = B + 1
1桁目のB = A + A は Bが「A-1」の数字なので 「A+Aの一桁目がA-1」になる値が当てはまる
9 + 9 = 18 「8 = 9 – 1」A = 9
B = 8
となる899 + 89 = 988
って考え方であってます?
— 六玉 ←これ推しマーク (@rottama_kyo) May 26, 2021
これでどうでしょうか? pic.twitter.com/Hwfwar0LOc
— よしマス (@Yoshimathe) May 26, 2021
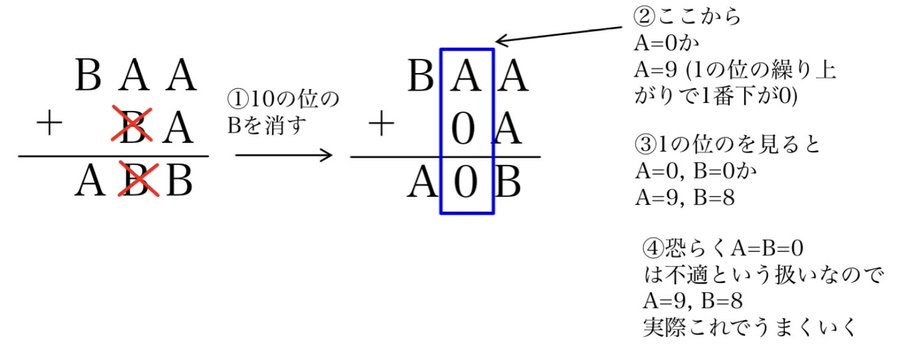
— みんてぃあ (@FH4M1N) May 26, 2021